Senin, 18 Februari 2019

MATEMATIKA

BAB 1
MATRIKS

1. Menganalisis konsep, nilai dererminan dan sifat operasi matriks, 
serta menerapkannya dalam menentukan invers matriks dan dalam 

memecahkan masalah.

Determinan Matriks

Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau 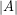\left| A \right|. Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
Untuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.

Determinan Matriks Ordo 2 x 2
Seperti yang sudah di ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]
Nilai determinan A disimbolkan dengan 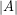\left| A \right|, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
  \[ det(A) \; = \; \left| A \right| = ad - bc \]

Contoh Soal:
Tentukan nilai determinan matriks
  \[ A \; = \; \begin{bmatrix} 3 & 1 \\ 2 & 5 \end{bmatrix} \]
Pembahasan:
  \[ \left| A \right| = ad - bc = 3 \cdot 5 - 1 \cdot 2 = 15 - 2 = 13\]

Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \]
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.

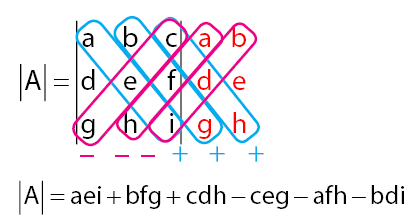
determinan matriks

Contoh perhitungan determinan pada matriks ordo 3:
  \[ \textrm{A} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]
Maka,
  \[ \left| \textrm{A} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]
  \[ \left| \textrm{A} \right| \; = 1\cdot 3 \cdot 2 + 2 \cdot 1 \cdot 2 + 1 \cdot 3 \cdot 1 - 2 \cdot 3 \cdot 1 - 1 \cdot 1 \cdot 1 - 2 \cdot 3 \cdot 2 \]
  \[ \left| \textrm{A} \right| \; = 6 + 4 + 3 - 6 - 1 - 12 \]
  \[ \left| \textrm{A} \right| \; = -6 \]

Selanjutnya, pembahasan kita akan berlanjut ke invers matriks.

Invers Matriks

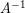Invers matriks dapat diartikan sebagai kebalikan dari suatu matriks tertentu. Jika suatu matriks bujur sangkar A dikalikan terhadap inversnya yaitu matriks bujur sangkar A^{-1} maka menghasilkan matriks I (matriks identitas pada operasi perkalian matriks).
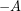Jika pada penjumlahan dua matriks, jumlah dua matriks bujur sangkar A dan -A akan menghasilkan matriks nol (matriks identitas pada operasi penjumlahan matriks).
  \[ A \cdot A^{-1} = I\]
  \[ A + (-A) = 0 \]

Invers Matriks Ordo 2 x 2
Invers dari suatu matirks A
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]
dinyatakan dalam rumus di bawah.
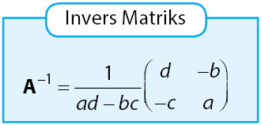
Invers Matriks
Contoh menentukan invers matriks A dapat dilihat seperti langkah-langkah berikut.
Diketahui:
  \[ \textrm{A} \; = \; \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \]
Tentukan invers dari matrik A!
Pembahasan:
  \[ \textrm{A}^{-1} \; = \; \frac{1}{3 \cdot 4 - 2 \cdot 1} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \frac{1}{12 - 2} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \frac{1}{10} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \begin{bmatrix}\frac{4}{10} & -\frac{2}{10} \\ -\frac{1}{10} & \frac{3}{10} \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \begin{bmatrix}\frac{2}{5} & -\frac{1}{5} \\ -\frac{1}{10} & \frac{3}{10} \end{bmatrix} \]

Invers Matriks Ordo 3 x 3
Cara untuk menentukan nilai invers matriks A dengan ordo 3 x 3 tidak sama dengan cara menentukan invers matriks dengan ordo 2 x 2. Cara menentukan invers matriks ordo 3 x 3 lebih rumit dari cara menentukan invers matriks 2 x 2. di bawah ini cara menentukan invers matriks ordo 3 x 3. Simak ulasannyna pada pembahasan di bawah.
Sebelum menentukan invers matriks ordo 3 x 3, perlu dipahami terlebih dahulu mengenai matriks minor, kofaktor, dan adjoin. Simak penjelasannya pada uraian di bawah.
  1. Matriks Minor
    Diketahui sebuah matriks A dengan ordo 3 seperti terlihat di bawah.

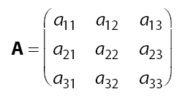    Invers Matriks Ordo 3 x 3
    Matriks minor M_{ij} adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2 seperti persamaan di bawah.

    Matriks Minor Mij
    Matriks-matriks minor di atas digunakan untuk mendapatkan matriks kofaktor A.

  2. Kofaktor
    Kofaktor baris ke-i dan kolom ke-j disimbolkan dengan C_{ij} dapat ditentukan dengan rumus seperti terlihat di bawah.
    Matriks Kofaktor
    Kofaktor di atas akan digunakan untuk menentukan adjoin matriks yang akan dicari nilai inversnya.

  3. Adjoin
    Secara umum, sebuah matriks memiliki matriks adjoin seperti ditunjukkan seperti pada matriks di bawah.
    Matriks Adjoin A
    Keterangan: C_{ij} adalah kofaktor baris ke-i dan kolom ke-j.
    Sehinnga, adjoin dari matriks A dinyatakan seperti terlihat pada persamaan di bawah.
      \[ Adj(A) \; = \; \; \begin{bmatrix} C_{11} & C_{21} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} \]

  4. Invers Matriks
    Bagian terakhir, bagian ini merupakan akhir dari proses mencari invers matriks dengan orde 3 atau lebih.
    Matriks minor, kofaktor, dan adjoin yang telah kita bahas di atas berguna untuk menentukan nilai invers dari suatu matriks dengan ordo matriks di atas 3 atau lebih. Secara umum, cara menentukan invers matriks dapat diperoleh melalui persamaan di bawah.
      \[ A^{-1} = \frac{1}{det(A)} \cdot Adj(A) \]
    Dengan substitusi nilai determinan matriks dan adjoin matriks maka akan diperoleh invers matriknya.
Agar lebih jelas, akan diberikan contoh soal cara mencari invers matriks berodo 3. Simak langkah-langkah yang diberikan di bawah.
Contoh soal menentukan invers matriks berordo 3 x 3
Tentukan invers matriks B yang diberikan pada persamaan di bawah.
  \[ \textrm{B} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]
Pembahasan:
Menghitung nilai determinan B:
  \[ \left| \textrm{B} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]
  \[ \left| \textrm{B} \right| \; = \; 1 \cdot 3 \cdot 2 + 2 \cdot 1 \cdot 2 + 1 \cdot 3 \cdot 1 - 2 \cdot 3 \cdot 1 - 1 \cdot 1 \cdot 1 - 2 \cdot 3 \cdot 2 \]
  \[ \left| \textrm{B} \right| \; = \; 6 + 4 + 3 - 6 - 1 - 12 = - 6 \]

Menentukan Kofaktor:
Berikut ini adalah hasil perhitungan nilai-nilai kofaktor untuk matriks B. Silahkan lihat kembali bagaimana cara mendapatkan nilai kofaktor pada rumus yang telah dibahas di atas jika belum hafal rumusnya.
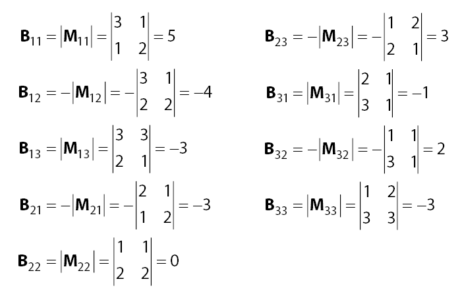
Matriks Kofaktor
Untuk menentukan invers B, kita membutuhkan matriks adjoin B. Sehingga, kita perlu menentukan matriks adjoin B terlebih dahulu.

Menentukan Adjoin B:
Adjoin dari matriks B, sesuai dengan persamaan di atas akan diperoleh hasil seperti berikut.
Matriks Adjoin B

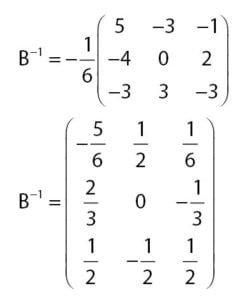
Menentukan Invers Matriks B:
Persamaan umum untuk invers suatu matriks dinyatakan melalui persamaan di bawah.
  \[ B^{-1} \; = \; \frac{1}{det(B)} \cdot Adj(B) \]
Sehingga, diperoleh invers matriks B seperti hasil berikut.
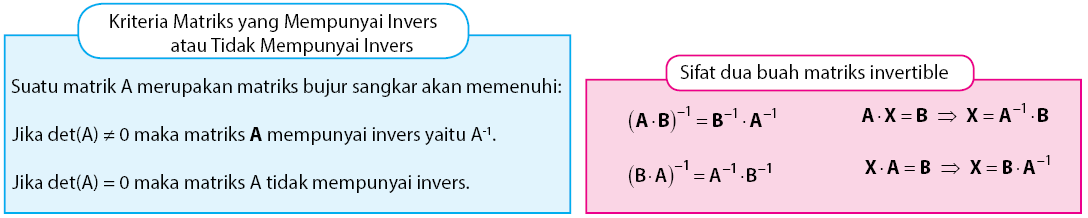
Invers Matriks B

Sifat-Sifat Matriks

Tidak semua matriks memiliki invers. Matriks yang memiliki invers dinamakan matriks nonsingular atau matriks invertible. Sedangkan matriks yang tidak memiliki invers dinamakan matriks singular. Kriteria matriks yang memiliki invers dapat dilihat pada gambar di bawah.
invers matriks

2. Menyajikan dan menyelaikan model Matematika dalam bentuk persamaan 
matriks dari suatu masalah nyata yang berkaitan dengan persamaan linear. 

Menyelesaikan SPLDV dengan Matriks

Cara yang paling umum dilakukan untuk menyelesaikan sistem persamaan linear dua variabel (SPLDV) adalah menggunakan metode substitusi, eliminasi, atau campuran, dan akan mengenalkan cara menyelesaiakan sistem persamaan linear (SPL) dengan cara yang baru, yaitu dengan menggunakan matriks. Meskipun cara ini akan sedikit rumit, namun cara ini akan sangat berguna untuk menyelesaikan sistem persamaan linear dengan banyak variabel. Selanjutnya, langsung ke langkah-langlah penyelesaian SPLDV yang dapat dilihat di bawah.
Diketahui sistem persamaan linear dua peubah sebagai berikut.
  \[ ax + by = c \]
            \[ px + qy = r \]
Dua persamaan di atas merupakan sistem persamaan linear dengan dua variabel, yaitu x dan y. Bentuk sistem di atas dalam matriks bisa dilihat pada persamaan di bawah.
  \[ \begin{bmatrix} a & b \\ p & q \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} c \\ r \end{bmatrix} \]
Berdasarkan sifat matriks invertibel, maka variabel x dan y dapat diketahui melalui cara berikut.
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a & b \\ p & q \end{bmatrix}^{-1} \begin{bmatrix} c \\ r \end{bmatrix} \]
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{aq - bp} \begin{bmatrix} q & -b \\ -q & a \end{bmatrix} \begin{bmatrix} c \\ r \end{bmatrix} \]
Atau juga bisa dengan cara seperti berikut.
  \[ x = \frac{D_{x}}{D} = \frac{\left| \begin{matrix} c & b \\ r & q \end{matrix} \right| }{\left| \begin{matrix} a & b \\ p & q \end{matrix} \right| }\]
  \[ y = \frac{D_{y}}{D} = \frac{\left| \begin{matrix} a & c \\ p & r \end{matrix} \right| }{\left| \begin{matrix} a & b \\ p & q \end{matrix} \right| }\]

Contoh soal sistem persamaan linear dua variabel yang diselesaikan menggunakan matriks dapat dilihat pada pembahasan di bawah.
Tentukan nilai x dan y yang memenuhi sistem persamaan linear:
  \[2x + y = 5 \]
  \[ x + y = 7 \]

Selanjutnya, akan diselesaikan SPLDV di atas menggunakan matriks. Bentuk matriks dari persamaan SPLDV pada soal adalah sebagai berikut.
  \[ \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 5 \\ 7 \end{bmatrix} \]
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} 5 \\ 7 \end{bmatrix} \]
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{2 \cdot 1 - 1 \cdot 1} \begin{bmatrix} 1 & -1 \\ - 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \end{bmatrix} \]
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{2 - 1} \begin{bmatrix} 1 & -1 \\ - 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \end{bmatrix} \]
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ - 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \end{bmatrix} \]
  \[ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -2 \\ 9 \end{bmatrix} \]
Jadi, solusi dari dua persamaan linear dua variabel 2x + y = 5 dan x + y = 7 adalah x = -2 dan y = 9.

Menyelesaikan SPLTV dengan Matriks

Cara menyelesaikan sistem persamaan linear menggunakan matriks akan sangat bermanfaat pada sistem persamaan linear dengan variabel yang banyak, misalnya pada sistem persamaan linear tiga variabel (SPLTV). Metode substitusi, eliminasi, atau campuran dirasa tidak tepat untuk menyelesaikan SPLTV. Selanjutnya, simak penyelesaian sistem persamaan linear tiga variabel (SPLTV) menggunakan matriks.
Diketahui tiga persamaan linear dengan tiga variabel (x, y, dan z) seperti terlihat pada persamaan di bawah.
  \[ ax + by + cz = d \]
  \[ px + qy + rz = s \]
  \[ kx + ly + mz = n \]

Bentuk SPLTV di atas dalam bentuk matriks dapat dibuat seperi berikut.
Cara Menyelesaikan Sistem Persamaan Linear (SPL) dengan Matriks

Berdasarkan matriks di atas, dapat disusun determinan utama, determinan variabel x, determinan variabel y, dan determinan variabel z. Untuk lebih jelasnya perhatikan masing-masing determinan pada daftar di bawah.
  1. Determinan utama
    Determinan Utama
  2. Determinan variabel x
    Determinan Variabel x
  3. Determinan variabel y
    Determinan Variabel y
  4. Determinan variabel z
    Determinan Variabel z
    5. Selanjutnya, untuk mengetahui niali masing-masing variabel x, y, dan z dapat mengunakan rumus berikut.

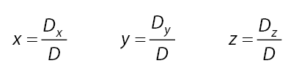
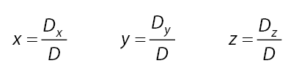
    Cara Menyelesaikan Sistem Persamaan Linear (SPL) dengan Matriks
    BAB 2
    BUNGA, PERTUMBUHAN DAN PELURUHAN

    1. Mendeskripsikan konsep barisan dan deret pada konteks dunia nyata, 
    seperti bunga, pertumbuhan, dan peluruhan. 

A. Bunga Tunggal dan Bunga Majemuk
A.1  BUNGA TUNGGAL
Pengertian Bunga
Bunga adalah jasa dari simpanan atau pinjaman yang dibayarkan pada akhir suatu jangka waktu yang ditentukan atas persetujuan bersama.

Pengertian Bunga Tunggal
Bunga tunggal adalah bunga yang timbul pada setiap akhir jangka waktu tertentu yang tidak mempengaruhi besarnya modal (besarnya modal tetap).

Besarnya bunga berbanding senilai dengan persentase dan lama waktunya dan umumnya berbanding senilai pula dengan besarnya modal.

Jika modal sebesar M dibungakan dengan bunga p % setahun maka:


B.     BUNGA MAJEMUK

Jika kita menyimpan modal berupa uang di bank selama periode bunga tertentu, misalnya satu tahun maka setelah satu tahun kita akan mendapatkan bunga sebesar p % kali modal yang kita bungakan. Jika bunga itu tidak kita ambil, tetapi ditambahkan pada modal awal untuk dibungakan lagi pada periode berikutnya, sehingga besarnya bunga pada setiap periode berikutnya berbeda jumlahnya (menjadi bunga berbunga), maka dikatakan modal tersebut dibungakan atas dasar bunga majemuk.

a.      Perbedaan Bunga Tunggal dan Bunga Majemuk
Bunga tunggal dihitung berdasarkan modal yang sama setiap periode sedangkan bunga majemuk dihitung berdasarkan modal awal yang sudah ditambahkan dengan bunga.

b.     Perhitungan Nilai Akhir Modal
a.      Dengan menggunakan rumus
Jika modal sebesar M dibungakan atas dasar bunga majemuk sebesar p % setahun selama n tahun, maka besarnya modal setelah n tahun adalah:

  • ·     Setelah satu tahun
                 
  •          Setelah dua tahun
           
  • Setelah n tahun


C.  Model Pertumbuhan Penduduk

            Penerapan deret ukur yang paling konvensional di bidang ekonomi adalah dalam hal penaksiran jumlah penduduk. Sebagaimana pernah dinyatakan oleh Malthus, penduduk dunia tumbuh mengikuti pola deret ukur. Secara matematik, hal ini dapat dirumuskan sebagai :
Pt = P1 R t-1
Dimana

R  = 1 + r
P1 = jumlah pada tahun pertama (basis)
Pt  = jumlah pada tahun ke-t
r    = persentase pertumbuhan per-tahun
t    = indeks waktu (tahun)                

Contoh Soal 1.
           
            Penduduk suatu kota berjumlah 1 juta pada tahun 1991, tingkat pertumbuhannya 4% per tahun. Hitunglah jumlah penduduk kota tersebut pada tahun 2006.

Jawaban :

P1 = 1.000.000
r = 0,04
R = 1,04
P2006 = P16= 1000000 (1,04)15
                = 1.000.000 ( 1,800943)
            = 1.800.943

Contoh Soal 2.
Jumlah penduduk kota X pada tahun 1994 mencapai 2 juta jiwa. Bila jumlah penduduk di kota tersebut meningkat dengan laju 2,5% pertahun dan andaikan laju pertambhan itu tetap sebesar itu dalam setiap tahunnya, tentukanlah banyaknya penduduk di kota X pada tahun 1999.

Penyelesaian :

Pertumbuhan penduduk pada dasarnya sama dengan pertambahan tabungan yang disimpan di Bank. Jadi, apabila banyaknya penduduk mula-mula P dengan tingkat kenaikan penduduk I%, sedangkan banyaknya penduduk setelah t tahun adalah Pt, maka tentunya banyaknya penduduk pada saat t tahun adalah :
Pt = P(1 + I)t

Jadi, dari soal di atas kita dapatkan, banyaknya penduduk di kota X pada tahun 1999 (setelah 5 tahun) menjadi :

P5 = 2.000.000 (1 + 0,025)5

= 2 . 106 . (1,025)5

Dengan bantuan kalkulator, kita dapatkan

P5 = 2 . 106 (1,025)5

=   2 . 106 (1,1314)

=   2.262.816 (dibulatkan). 


    BAB 3
    INDUKSI MATEMATIKA


    Induksi matematika adalah suatu metode pembuktian deduktif yang digunakan untuk membuktikan pernyataan matematika yang bergantung pada himpunan bilangan yang terurut rapi (well ordered set), seperti bilangan asli ataupun himpunan bagian tak kosong dari bilangan asli.

    Perlu ditekankan bahwa induksi matematika hanya digunakan untuk membuktikan kebenaran dari suatu pernyataan atau rumus, bukan untuk menurunkan rumus. Atau lebih tegasnya induksi matematika tidak dapat digunakan untuk menurunkan atau menemukan rumus.

    Berikut beberapa contoh pernyataan matematika yang dapat dibuktikan dengan induksi matematika :
    P(n) :  2 + 4 + 6 + ... + 2n = n(n + 1), n bilangan asli
    P(n) :  6n + 4 habis dibagi 5, untuk n bilangan asli.
    P(n) :  4n < 2n, untuk setiap bilangan asli n ≥ 4

    Cara yang paling mudah untuk memahami prinsip kerja induksi matematika adalah dengan mengamati efek domino. Kita dapat mulai dengan mengajukan pertanyaan "kapan semua domino akan jatuh".


    Ada dua kondisi yang harus dipenuhi agar semua domino tersebut jatuh.
    Pertama : domino 1 harus jatuh.
    Kedua : benar bahwa setiap domino yang jatuh akan menjatuhkan tepat satu domino berikutnya. Artinya jika domino 1 jatuh maka domino 2 pasti jatuh, jika domino 2 jatuh maka domino 3 pasti jatuh dan seterusnya. Secara umum dapat kita katakan jika domino k jatuh maka domino (k + 1) juga jatuh dan implikasi ini berlaku untuk semua domino.

    Jika kedua kondisi diatas telah terpenuhi, sudah dipastikan semua domino akan jatuh.


    Prinsip Induksi Matematika

    Misalkan P(n) adalah suatu pernyataan yang bergantung pada n. P(n) benar untuk setiap n bilangan asli jika memenuhi 2 kondisi berikut :
    1. P(1) benar, artinya untuk n = 1 maka P(n) bernilai benar.
    2. Untuk setiap bilangan asli k, jika P(k) benar maka P(k + 1) juga benar.
    Prinsip diatas dapat diperluas untuk pernyataan yang bergantung pada himpunan bagian tak kosong dari bilangan asli.

    Perluasan Prinsip Induksi Matematika
    Misalkan P(n) adalah suatu pernyataan yang bergantung pada n. P(n) benar untuk setiap bilangan asli n ≥ m jika memenuhi 2 kondisi berikut :
    1. P(m) benar, artinya untuk n = m, maka P(n) bernilai benar
    2. Untuk setiap bilangan asli k ≥ m, jika P(k) benar maka P(k + 1) juga benar.

    Untuk menunjukkan P(1) benar, kita cukup mensubstitusikan n = 1 pada P(n). Jika P(n) disajikan dalam bentuk persamaan, berarti ruas kiri harus sama dengan ruas kanan pada saat n = 1, barulah kita simpulkan P(1) benar. Cara yang sama dapat kita terapkan untuk menunjukkan P(m) benar.

    Kembali lagi pada kasus domino diatas, agar domino (k + 1) jatuh, terlebih dahulu domino k harus jatuh, barulah implikasi "jika domino k jatuh maka domino (k + 1) jatuh" dapat terjadi.

    Jadi, untuk menunjukkan implikasi "jika P(k) benar maka P(k + 1) benar", terlebih dulu kita harus menganggap atau mengasumsikan bahwa P(k) benar. Kemudian berdasarkan asumsi tersebut kita tunjukkan P(k + 1) juga benar. Proses asumsi P(k) benar ini disebut dengan hipotesis induksi.

    Untuk menunjukkan P(k + 1) benar, dapat kita mulai dari hipotesis, yaitu dari asumsi P(k) benar ataupun dari kesimpulan, yaitu dari P(k + 1) itu sendiri.

    Langkah-Langkah Pembuktian Induksi Matematika

    Dari uraian-uraian diatas, langkah-langkah pembuktian induksi matematika dapat kita urutkan sebagai berikut :
    1. Langkah dasar : Tunjukkan P(1) benar.
    2. Langkah induksi : Asumsikan P(k) benar untuk sebarang k bilangan asli, kemudian tunjukkan P(k+ 1) juga benar berdasarkan asumsi tersebut. 
    3. Kesimpulan : P(n) benar untuk setiap bilangan asli n.

    Pembuktian Deret

    Sebelum masuk pada pembuktian deret, ada beberapa hal yang perlu dipahami dengan baik menyangkut deret.

    Jika P(n) :  u1 + u2 + u3 + ... + un = Sn , maka
    P(1) :  u1 = S1
    P(k) :  u1 + u2 + u3 + ... + uk = Sk
    P(k + 1) :  u1 + u2 + u3 + ... + uk + uk+1 = Sk+1

    Contoh 1
    Buktikan 2 + 4 + 6 + ... + 2n = n(n + 1), untuk setiap n bilangan asli.

    Jawab :
    P(n) :  2 + 4 + 6 + ... + 2n = n(n + 1)
    Akan dibuktikan P(n) benar untuk setiap n ∈ N

    Langkah Dasar :
    Akan ditunjukkan P(1) benar
    2 = 1(1 + 1)
    Jadi, P(1) benar

    Langkah Induksi :
    Asumsikan P(k) benar yaitu
    2 + 4 + 6 + ... + 2k = k(k + 1),    k ∈ N

    Akan ditunjukkan P(k + 1) juga benar, yaitu
    2 + 4 + 6 + ... + 2k + 2(k + 1) = (k + 1)(k + 1 + 1)

    Dari asumsi :
    2 + 4 + 6 + ... + 2k = k(k + 1)
    Tambahkan kedua ruas dengan uk+1 :
    2 + 4 + 6 + ... + 2k + 2(k + 1) = k(k + 1) + 2(k + 1)
    2 + 4 + 6 + ... + 2k + 2(k + 1) = (k + 1)(k + 2)
    2 + 4 + 6 + ... + 2k + 2(k + 1) = (k + 1)(k + 1 + 1)
    Jadi, P(k + 1) benar

    Berdasarkan prinsip induksi matematika, terbukti bahwa P(n) benar untuk setiap n bilangan asli.


    Contoh 2
    Buktikan 1 + 3 + 5 + ... + (2n − 1) = n2 benar, untuk setiap n bilangan asli

    Jawab :
    P(n) :  1 + 3 + 5 + ... + (2n − 1) = n2
    Akan ditunjukkan P(n) benar untuk setiap n ∈ N

    Langkah Dasar :
    Akan ditunjukkan P(1) benar
    1 = 12
    Jadi, P(1) benar

    Langkah Induksi :
    Asumsikan P(k) benar, yaitu
    1 + 3 + 5 + ... + (2k − 1) = k2,    k ∈ N

    Akan ditunjukkan P(k + 1) juga benar, yaitu
    1 + 3 + 5 + ... + (2k − 1) + (2(k + 1) − 1) = (k + 1)2

    Dari asumsi :
    1 + 3 + 5 + ... + (2k − 1) = k2
    Tambahkan kedua ruas dengan uk+1 :
    1 + 3 + 5 + ... + (2k − 1) + (2(k + 1) − 1) = k2 + (2(k + 1) − 1)
    1 + 3 + 5 + ... + (2k − 1) + (2(k + 1) − 1) = k2 + 2k + 1
    1 + 3 + 5 + ... + (2k − 1) + (2(k + 1) − 1) = (k + 1)2
    Jadi, P(k + 1) juga benar

    Berdasarkan prinsip induksi matematika, terbukti bahwa P(n) benar untuk setiap n bilangan asli.


    Pembuktian Keterbagian

    Pernyataan "a habis dibagi b" bersinonim dengan :
    • a kelipatan b
    • b faktor dari a
    • b membagi a
      Jika p habis dibagi a dan q habis dibagi a, maka (p + q) juga habis dibagi a.
      Sebagai contoh, 4 habis dibagi 2 dan 6 habis dibagi 2, maka (4 + 6) juga habis dibagi 2
      Contoh 3
      Buktikan 6n + 4 habis dibagi 5, untuk setiap n bilangan asli.

      Jawab :
      P(n) :  6n + 4 habis dibagi 5
      Akan dibuktikan P(n) benar untuk setiap n ∈ N.

      Langkah Dasar :
      Akan ditunjukkan P(1) benar
      61 + 4 = 10 habis dibagi 5
      Jadi, P(1) benar

      Langkah Induksi :
      Asumsikan P(k) benar, yaitu
      6k + 4 habis dibagi 5,    k ∈ N

      Akan ditunjukkan P(k + 1) juga benar, yaitu
      6k+1 + 4 habis dibagi 5.

      6k+1 + 4 = 6(6k)+ 4
      6k+1 + 4 = 5(6k) + 6k + 4

      Karena 5(6k) habis dibagi 5 dan 6k + 4 habis dibagi 5, akibatnya 5(6k) + 6k + 4 juga habis dibagi 5.
      Jadi, P(k + 1) benar.

      Berdasarkan prinsip induksi matematika, terbukti bahwa 6n + 4 habis dibagi 5, untuk setiap n bilangan asli.


      Bilangan bulat a habis dibagi bilangan bulat b jika terdapat bilangan bulat m sehingga berlaku a = bm.
      Sebagai contoh, "10 habis dibagi 5" benar karena terdapat bilangan bulat m = 2 sehingga 10 = 5.2. Jadi, pernyataan "10 habis dibagi 5" dapat kita tulis menjadi "10 = 5m, untuk m bilangan bulat"
      Berdasarkan konsep diatas, pembuktian keterbagian dapat pula diselesaikan dengan cara sebagai berikut.

      Contoh 4
      Buktikan n3 + 2n habis dibagi 3, untuk setiap n bilangan asli

      Jawab :
      P(n) :  n3 + 2n = 3m, dengan m ∈ Z
      Akan dibuktikan P(n) benar untuk setiap n ∈ N

      Langkah Dasar :
      Akan ditunjukkan P(1) benar
      13 + 2.1 = 3 = 3.1
      Jadi, P(1) benar

      Langkah Induksi :
      Asumsikan P(k) benar, yaitu
      k3 + 2k = 3m,    k ∈ N

      Akan ditunjukkan P(k + 1) juga benar, yaitu
      (k + 1)3 + 2(k + 1) = 3p,     p ∈ Z

      (k + 1)3 + 2(k + 1) = (k3 + 3k2 + 3k + 1) + (2k + 2)
      (k + 1)3 + 2(k + 1) = (k3 + 2k) + (3k2 + 3k + 3)
      (k + 1)3 + 2(k + 1) = 3m + 3(k2 + k + 1)
      (k + 1)3 + 2(k + 1) = 3(m + k2 + k + 1)

      Karena m bilangan bulat dan k bilangan asli, maka (m + k2 + k + 1) adalah bilangan bulat.
      Misalkan p = (m + k2 + k + 1), maka
      (k + 1)3 + 2(k + 1) = 3p, dengan p ∈ Z
      Jadi, P(k + 1) benar

      Berdasarkan prinsip induksi matematika, terbukti bahwa n3 + 2n habis dibagi 3,  untuk setiap n bilangan asli.

      Pembuktian Pertidaksamaan

      Berikut sifat-sifat pertidaksamaan yang sering digunakan
      1.  Sifat transitif
           a > b > c  ⇒  a > c  atau
           a < b < c  ⇒  a < c

      2.  a < b dan c > 0  ⇒  ac < bc  atau
           a > b dan c > 0  ⇒  ac > bc

      3.  a < b  ⇒  a + c < b + c  atau
           a > b  ⇒  a + c > b + c

      Sebelum masuk pada contoh soal, ada baiknya kita latihan menggunakan sifat-sifat diatas untuk menunjukkan implikasi "jika P(k) benar maka P(k + 1) juga benar".

      Misalkan
      P(k) :  4k < 2k
      P(k + 1) :  4(k + 1) < 2k+1
      Jika diasumsikan P(k) benar untuk k ≥ 5, tunjukkan P(k + 1) juga benar !

      Ingat bahwa target kita adalah menunjukkan
      4(k + 1) < 2k+1 = 2(2k) = 2k + 2k  (TARGET)

      Kita dapat mulai dari ruas kiri pertaksamaan diatas
      4(k + 1) = 4k + 4
      4(k + 1) < 2k + 4        (karena 4k < 2k)
      4(k + 1) < 2k + 2k      (karena 4 < 4k < 2k)
      4(k + 1) = 2(2k)
      4(k + 1) = 2k+1

      Berdasarkan sifat transitif kita simpulkan
      4(k + 1) < 2k+1

      Mengapa 4k dapat berubah menjadi 2k ?
      Berdasarkan sifat 3, kita diperbolehkan menambahkan kedua ruas suatu pertaksamaan dengan bilangan yang sama, karena tidak akan merubah nilai kebenaran pertaksamaan tersebut. Karena 4k < 2k benar, akibatnya 4k + 4 < 2k + 4 juga benar.

      Darimana kita tahu, 4 harus diubah menjadi 2k ?
      Perhatikan target. Hasil sementara kita adalah 2k + 4 sedangkan target kita adalah 2k + 2k.
      Untuk k ≥ 5, maka 4 < 4k dan 4k < 2k adalah benar, sehingga 4 < 2k juga benar (sifat transitif). Akibatnya 2k + 4 < 2k + 2k  benar (sifat 3).


      Contoh 5
      Buktikan untuk setiap bilangan asli n ≥ 4 berlaku
      3n < 2n

      Jawab :
      P(n) :  3n < 2n
      Akan dibuktikan P(n) berlaku untuk n ≥ 4, n ∈ N

      Langkah Dasar :
      Akan ditunjukkan P(4) benar
      3.4 = 12 < 24 = 16
      Jadi, P(4) benar

      Langkah Induksi :
      Asumsikan P(k) benar, yaitu
      3k < 2k,    k ≥ 4

      Akan ditunjukkan P(k + 1) juga benar, yaitu
      3(k + 1) < 2k+1

      3(k + 1) = 3k + 3
      3(k + 1) < 2k + 3               (karena 3k < 2k)
      3(k + 1) < 2k + 2k             (karena 3 < 3k < 2k)
      3(k + 1) = 2(2k)
      3(k + 1) = 2k+1

      Jadi, P(k + 1) juga benar

      Berdasarkan prinsip induksi matematika, terbukti bahwa P(n) berlaku untuk setiap bilangan asli n ≥ 4.


      Contoh 6
      Buktikan untuk setiap bilangan asli n ≥ 2 berlaku
       3n > 1 + 2n

      Jawab :
      P(n) :  3n > 1 + 2n
      Akan dibuktikan P(n) berlaku untuk n ≥ 2, n ∈ N

      Langkah Dasar :
      Akan ditunjukkan P(2) benar
      32 = 9 > 1 + 2.2 = 5
      Jadi, P(1) benar

      Langkah Induksi :
      Asumsikan P(k) benar, yaitu
      3k > 1 + 2k,    k ≥ 2

      Akan ditunjukkan P(k + 1) juga benar, yaitu
      3k+1 > 1 + 2(k + 1)

      3k+1 = 3(3k)
      3k+1 > 3(1 + 2k)               (karena 3k > 1 + 2k)
      3k+1 = 3 + 6k
      3k+1 > 3 + 2k                    (karena 6k > 2k)
      3k+1 = 1 + 2k + 2
      3k+1 = 1 + 2(k + 1)

      Jadi, P(k + 1) juga benar

      Berdasarkan prinsip induksi matematika, terbukti bahwa P(n) berlaku untuk setiap bilangan asli n ≥ 2.


      Contoh 7
      Buktikan untuk setiap bilangan asli n ≥ 5 berlaku
       2n − 3 < 2n-2

      Jawab :
      P(n) :  2n − 3 < 2n-2
      Akan dibuktikan P(n) berlaku untuk n ≥ 5, n ∈ N

      Langkah Dasar :
      Akan ditunjukkan P(5) benar
       2.5 − 3 = 7 < 25-2 = 8
      Jadi, P(1) benar

      Langkah Induksi :
      Asumsikan P(k) benar, yaitu
      2k − 3 < 2k-2 ,    k ≥ 5

      Akan ditunjukkan P(k + 1) juga benar, yaitu
      2(k + 1) − 3 < 2k+1-2

      2(k + 1) − 3 = 2k + 2 − 3
      2(k + 1) − 3 = 2k − 3 + 2
      2(k + 1) − 3 < 2k-2 + 2         (karena 2k − 3 < 2k-2)
      2(k + 1) − 3 < 2k-2 + 2k-2     (karena 2 < 2k − 3 < 2k-2)
      2(k + 1) − 3 = 2(2k-2)
      2(k + 1) − 3 = 2k+1-2

      Jadi, P(k + 1) juga benar

      Berdasarkan prinsip induksi matematika, terbukti bahwa P(n) berlaku untuk setiap bilangan asli n ≥ 5.


      Contoh 8
      Buktikan untuk setiap bilangan asli n ≥ 4 berlaku
      (n + 1)! > 3n

      Jawab :
      P(n) :  (n + 1)! > 3n
      Akan dibuktikan P(n) berlaku untuk n ≥ 4, n ∈ N

      Langkah Dasar :
      Akan ditunjukkan P(4) benar
      (4 + 1)! > 34
      ruas kiri : 5! = 5.4.3.2.1 = 120
      ruas kanan : 34 = 81
      Jadi, P(1) benar

      Langkah Induksi :
      Asumsikan P(k) benar, yaitu
      (k + 1)! > 3k ,   k ≥ 4

      Akan ditunjukkan P(k + 1) juga benar, yaitu
      (k + 1 + 1)! > 3k+1

      (k + 1 + 1)! = (k + 2)!
      (k + 1 + 1)! = (k + 2)(k + 1)!
      (k + 1 + 1)! > (k + 2)(3k)            (karena (k + 1)! > 3k)
      (k + 1 + 1)! > 3(3k)                     (karena k + 2 > 3)
      (k + 1 + 1)! = 3k+1

      Jadi, P(k + 1) juga benar

      Berdasarkan prinsip induksi matematika, terbukti bahwa P(n) berlaku untuk setiap bilangan asli n ≥ 4.

    Diposting oleh di

    1 komentar:

    1. dinda prastuty20 Februari 2019 pukul 23.17

      Antum luar biasa. Bisa menyajikan materi dengan baik. Tinggal antum coba baca dengan seksama dan coba latihan soal yang terkait, ya. Semoga memudahkan antum dalam penyelesaian ujian nanti.
      Salam sukses mulia.

      BalasHapus

    Langganan: Posting Komentar (Atom)